푸앵카레의 추측(Poincaré conjecture)
2000년 클레이 수학연구소에서 제시한 밀레니엄 문제 중 하나이다. 말하자면 "단일 연결인 3차원 다양체는 구면과 같다."는 명제로 풀어서 말하자면 "어떤 닫힌 3차원 공간에서 모든 폐곡선이 수축되어 한 점이 될 수 있다면 이 공간은 반드시 3차원 구(3 dimensional sphere)로 변형될 수 있다는 뜻이다."
1904년 푸앵카레가 제시한 이래 100여년 간 수학자들을 괴롭히다가 러시아의 수학자 페렐만에 의해 해결되었다. 앙리 푸앵카레는 레몽 푸앵카레의 사촌으로 레몽은 프랑스의 대통령이었다.
형태의 수수께끼에 다가선 푸앵카레 추측
사람들은 마젤란의 세계 일주를 보고 지구가 둥글다는 것이 실증된 것이라고 했다. 하지만 푸앵카레는 그것으로는 지구가 둥글다는 것을 증명할 수 없다고 했다.
"만일 지구가 둥근 공모양이 아니라면 어땠을까? 가령 북극과 남극을 관통하는 큰 구멍이 뚫린 도넛 같으 모양이었다면? 그렇더라도 마젤란의 함대는 같은 장소로 돌아올 수 있는게 아닌가! 그러니까 같은 장소로 돌아왔다고 해서 이 세계가 동그란 공 모양이라고 단언할 수는 없다!"
그러면 밧줄 하나를 가지고 사고 실험을 해보자.
"먼저 머릿속으로 아주아주 긴 밧줄을 준비해서 곶에 섭니다. 그리고 밧줄 한쪽 끝을 곶에 단단히 고정시키고, 다른 한 쪽 끝은 배에 묶습니다. 그리고 밧줄을 매단 배를 타고 긴 항해를 떠나는 겁니다. 배는 지구를 돌아 마침내 처음 출발한 장소로 되돌아옵니다. 자, 이제 여러분은 배에 묶었던 밧줄을 풀러 그것을 다시 곶에 고정시킵니다. 이 밧줄을 끌어당겨서 모두 회수할 수 있다면 지구는 둥글다고 할 수 있습니다. 푸앵카레는 그렇게 생각한 것입니다."

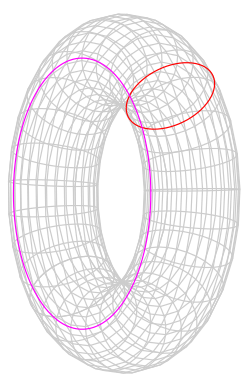
"그렇다면 이번에는 만일 지구가 도넛 모양이라면 어떻게 될지 생각해보자. 지구에 두른 밧줄을 다시 댕겨보자. 구멍속으로 밧줄을 통과시켜서 두르면 밧줄이 지구에 걸려서 회수할 수 없다. 그리고 구엄을 따라 밧줄을 두른 경우에도 역시 회수할 수 없다. 밧줄이 공중에 뜨기 때문이다. 지구표면을 따라서 밧줄을 회수하지 않는 한 지구의 모양을 찾아냈다고 말할 수는 없다."
'경직된 수학' 미분기하학 vs '유연한 수학' 위상기하학
위상기하하겡서는 구와 원쁠과 원기둥은 전부 '같은 모양'이 된다. 높이와 반지름이 다르다는 이유로 원뿔을 일일이 구별하지 않는다. 토폴로지에서는 구멍의 개수가 중요하다. 더 자세히 들어가보면 구멍의 수가 아닌 표면의 형태가 중요하다.
수학에 있어서의 차원 (UC 버클리대 교수 스티븐 스메일)
그것이 '수학적으로 보는 법'입니다.
수학적으로 3차원을 기술할 수 있다면 고차원으로 갈 때, 예를 들어 5차원인 경우 숫자 다섯 개를 사용하면 됩니다.
수학이라는 틀 안에서 고차원을 생각하는 것은 쉬운 일입니다.
20차원 공간의 도면을 무리하게 머리에 그릴 필요도 없습니다.
수학은 언어입니다."
고차원으로 떠나는 여행
3차원 우주문제인 푸앵카레 추측을 높은 차원부터 순서대로 공략한다는 스메일 박사의 시도는 높이 평가받아 1966년 필즈상을 수상했다. 논문의 제목은 「고차원에서 일반회된 푸앵카레 추측」으로 "만일 N 차원(N=3,4 차원 이외)의 우주에 두른 밧줄을 모두 회수할 수 있다면 N 차원 우주는 둥글다." 이 증명은 5차원보다 차원이 높은 우주에 한해서만 성립하므로 3차원에서 기술된 본래의 푸앵카레 추측을 해결한 것은 아니었다.
어찌되었건 스메일 박사의 증명으로 푸앵카레 추측 연구에는 '고차원 우주'로 가는 문이 활짝 열렸다. 그 바로 뒤에 존 스털링스 박사가 완전히 다른 접근법으로 '7차원 이상의 우주'에서 푸앵카레 추측을 증명했고, 나아가 영국의 에릭 크리스토퍼 지먼 박사가 '5, 6차원 우주'에서 푸앵카레 추측을 증명해보였다. 그리고 마이클 프리드먼 박사가 "가령 우주가 4차원 공간이라면 역시 밧줄이 얽히지 않은 상태로 회수할 수 있다."는 것을 증명해 역시 필즈상을 수상했다.
2005년 결국 3차원에서도 페렐만에 의해 100년의 난제 푸앵카레의 추측이 풀렸음이 선언되었다.
 |
|
'반서재 Antilibrary' 카테고리의 다른 글
| 니시우치 히로무, 「빅데이터를 지배하는 통계의 힘」- 3장. 오차와 인과관계가 통계학의 핵심이다. (0) | 2014.04.29 |
|---|---|
| 야노 쇼,「꿈이 있는 공부는 배신하지 않는다」- 내가 누군인지 공부하는 이유 (0) | 2014.04.29 |
| 마크 쉔, 크리스틴 로버그, 「편안함의 배신」- 불편에 대한 내성은 생각보다 크다 (에필로그) (0) | 2014.04.24 |
| 마크 쉔, 크리스틴 로버그, 「편안함의 배신」- 실현될 때까지 연기하기 (0) | 2014.04.24 |
| 마크 쉔, 크리스틴 로버그, 「편안함의 배신」- 이중성(duality)의 달성 (0) | 2014.04.24 |